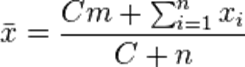- Category: July 2015: Real (Right)-Time Marketing
 Performing marketing in real-time requires a well planned calculated and orchestrated approach to a particular customer at a specific time and place and that is where the Bayesian probability could come into play, since it allows for decision making and market research evaluation under uncertainty and with limited data. Although considered impractical until the mid-1980s, the method gained in importance in marketing primarily due to the birth and widespread use of the internet.
Performing marketing in real-time requires a well planned calculated and orchestrated approach to a particular customer at a specific time and place and that is where the Bayesian probability could come into play, since it allows for decision making and market research evaluation under uncertainty and with limited data. Although considered impractical until the mid-1980s, the method gained in importance in marketing primarily due to the birth and widespread use of the internet.
In contrast to interpreting probability as the "frequency" or "propensity" of some phenomenon, Bayesian probability is a quantity that we assign for representing a state of knowledge, or a state of belief. Hence, it can be seen as an extension of propositional logic that enables reasoning with hypotheses, i.e., the propositions whose truth or falsity is uncertain.
Broadly speaking, there are two views on Bayesian probability that interpret the 'probability' concept in different ways:
• For objectivists, probability objectively measures the plausibility of propositions, i.e. the probability of a proposition corresponds to a reasonable belief everyone (even a "robot") sharing the same knowledge should share in accordance with the rules of Bayesian statistics, which can be justified by requirements of rationality and consistency.
• For subjectivists, probability corresponds to a 'personal belief', which means rationality and coherence constrain the probabilities a subject may have, but allow for substantial variation within those constraints.
To meet the needs of science and of human limitations, Bayesian statisticians have developed "objective" methods for specifying prior probabilities, since personal probabilities are problematic for science and for some applications where decision-makers lack the knowledge or time to specify an informed probability distribution (on which they are prepared to act).
To no surprise, Bayesian methods are widely accepted and used, such as in the field of machine learning, since statisticians have no other choice than either to use informed priors (using relevant expertise or previous data) or to choose among the competing methods for constructing "objective" priors.
Calculating the Bayesian average uses the prior mean m and a constant C, whereby C is assigned a value that is proportional to the typical data set size. The value is larger when the expected variation between data sets (within the larger population) is small. It is smaller, when the data sets are expected to vary substantially from one another.